The physics of miracles, Part 1
How the laws of thermodynamics can help us understand a physical basis for (some) miracles.
This is a repost from my old blog, updated and expanded. Back when I first posted this, I had intended to follow up quickly with Part 2, which focuses on miracles in the context of the stochastic weirdness of quantum mechanics. I never got around to it. This time, I intend to get around to it.
Miracles are part of Christian tradition that are often ridiculed, or at least heavily doubted, by non-believers. Here’s how it usually goes. Scripture describes God or one of God’s agents doing the impossible, and since impossible things never happen according to the laws of nature, how can any reasonable person believe in something as nonsensical as miracles?
But is that really what all miracles are—defying the laws of nature and doing the impossible? I don’t think so.
When I first taught statistical thermodynamics to my university students, it got me thinking about how probability plays a role in a lot of natural phenomena. There are events any reasonable person would consider impossible, but in terms of the laws of physics, they have an extremely small but not strictly zero probability of occurring. (This is as true of quantum mechanics as it is of statistical mechanics, and I’ll get into that in the second part of this series.)
But what physics and probabilities really got me thinking about were miracles. What if most miracles aren’t impossible events, just highly improbable events? If so, then whoever is performing the miracle would need inside access to the mechanics of the natural world and the power to manipulate things. It’s actually not that difficult to imagine. To see how this would work, let’s consider another probabilistic scenario—the lottery.
In 2015, a man named Eddie Tipton was convicted of two counts of fraud for rigging the system of the Iowa state lottery. He had used a clever bit of software, called a rootkit, to make certain sequences of numbers much more likely to come up in the drawings on particular days. Rootkit software, properly executed, is installed into a system using a USB thumb drive, it does its business, and then deletes itself to remove incriminating evidence.
You might well wonder, with supposedly no evidence of tampering remaining in the lottery system, why was Tipton even suspected of lottery fraud, let alone arrested and convicted? The reason is simple. He was the information security chief for a multi-state lottery corporation, and the winning ticket, worth over $16 million, had been purchased by him.
The prosecutor explained to the jury deliberating Tipton’s case that they didn’t have to understand how the rootkit or the complicated lottery system worked in order to pass a guilty conviction. All they had to understand was that it was virtually impossible that someone with access to the state’s lottery system would win the big jackpot purely by coincidence. It was enough to convince the jury to find Tipton guilty of fraud.
If Eddie Tipton had not defrauded the lottery system, you could reasonably describe his winning the big jackpot as miraculous. It’s not like someone winning the lottery is in itself miraculous—there are legitimate winners of big lottery jackpots every week—but for someone with access to the lottery system to win completely by chance is so unlikely that no one believes it could really happen.
Now, what if what I’ve just described—having skills, inside access, and knowledge of the system to produce a pre-intended outcome—is, at its core, how many miracles actually occur?
Before we get into the physics, let’s first go to scripture to see how miracles are defined.
There are two Hebrew words translated as ‘miracle’ in the Old Testament. They are
oth: this word refers to a sign. The purpose of this sort of miracle is to draw people’s attention to God. (e.g. Exodus 12:13)
mopheth: this word refers to a wonder and is often used together with oth (signs and wonders). The purpose of this sort of miracle is to display God’s power. (e.g. Exodus 7:3)
The Greek counterparts in the New Testament are
semeion: this word refers to a sign, and is used to describe acts that are evidence of divine authority, usually something that goes against the usual course of nature (e.g. John 2:11). (From this word we get the word “semiotics,” the study of signs and symbols.)
teras: this word refers to a wonder, and is used to describe something that causes a person to marvel (e.g. Acts 2:22)
There are two additional words used for miracle in the New Testament:
dunamis: this word refers to an act that is supernatural in origin (e.g. Mark 6:2)
ergon: this word means “work,” as in the works of Jesus (e.g. Matthew 11:2). (From this word we get the word “erg,” which in physics is a unit of energy, like joules or calories.)
With that in mind, let’s talk about the physics of miracles.
Is it possible to square some miracles with the laws of nature without detracting from their wondrousness? I believe the answer is yes, as you’ll see below.
Statistical thermodynamics deals with predictions about the behavior of systems with enormous numbers of particles. These numbers are so huge that no one could be certain about predictions for individual particles. This is where statistics come to the rescue, as you can easily make statistical predictions about entire systems of particles. The interesting thing is, the more particles you’re dealing with, the less able you are to make predictions about any particular particle, but the more accurate your predictions about the entire system become. And this is precisely what relates to miracles that do not violate the laws of nature.
The laws of nature permit a lot more than most people realize. In our everyday lives, we don’t usually define common sense expectations in terms of probabilities, but that’s often precisely what common sense is. In thermodynamics, that which constitutes our everyday expectation in any given situation is what’s referred to as the most probable state of a system.
To see what I mean, let’s consider a room with air in it, and imagine that we divide the room into two equal parts. We’ll also imagine this room and the air molecules comprise a closed system: the room has been effectively sealed off with its doors and windows closed for several hours, with no energy or air added to or removed from it. This means the room has had time for the air particles to jostle around and distribute themselves randomly. What we expect when we walk into the room is that the air molecules will be relatively evenly distributed throughout the room with approximately the same number of molecules on either side. What we don’t expect is that all of the air molecules will be on one side of the room with a vacuum on the other side. Most of you probably couldn’t explain why you’d be astonished to find all of the air on just one side of the room—you intuitively sense that this would be extremely odd—but there is a sound reason for this expectation that’s rooted in probability.
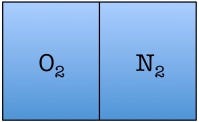
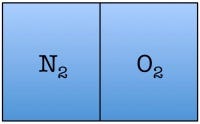
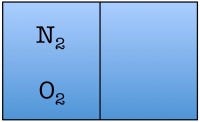
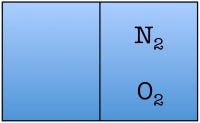
Let’s construct what scientists call a toy model—a simplified example of a situation that helps you to understand the fundamentals. Our toy model consists of a room divided in half with only two air molecules in it: a diatomic oxygen molecule and a diatomic nitrogen molecule. Here are the possible arrangements of these molecules:
Each possible arrangement is called a “state” of the room. We see that there are four possible states for the room. There are two states in which the air molecules are distributed evenly in the room, and two in which both of the air molecules are on one side of the room. The probability of finding a room in a state in which both molecules are on one side of the room is 2 out of 4, or 50%.
Easy enough. But things start to change quickly when we add more particles.
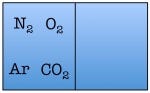
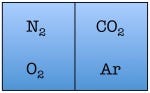
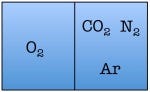
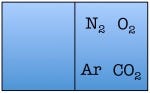
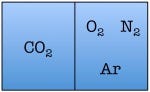
Let’s see what happens when we double the number of particles to four—one each of diatomic nitrogen, diatomic oxygen, argon, and carbon dioxide.
and so on, for a total of 16 possible states for the room. Again, there are only two states in which the air molecules are on one side of the room, but now there are many more total possible states than before. The probability of all four molecules spontaneously arranging themselves on one side of the room is 2 out of 16, or 12.5%. This is a lot less probable than in the previous example, but not so low that you would be astonished to find all of the air molecules on one side of the room.
Based on this toy model, we can write the mathematical expression for the total number of possible arrangements of air molecules in a two-sided room as
total # of states = (2 sides of the room)# of molecules
That’s 2 to the power of the number of molecules in the room, which we’ll call N. More simply expressed, this is
2N
That’s 2 raised to the power of the number of molecules, N. For the two-molecule example, that’s 22 = 4, and for the four-molecule example, that’s 24 = 16.
Let’s consider a room with N = 100 air molecules in it, and calculate the probability of finding all of the molecules on one side of the room:
total # of permutations = 2100 = 1030
Even with a relatively paltry 100 air molecules in the room, the probability of finding them all on one side of the room is a ridiculously low 2 out of 1030 possible permutations.
Let’s put this in perspective. If the air molecules randomly redistribute themselves every second, you’d have to wait a trillion lifetimes of the universe before you’d have a reasonable expectation of finding all 100 air molecules on one side of the room.
Let’s now consider a typical room, which has not 100, not 1,000, not even a billion air molecules in it, but a whopping N = 1027 air molecules in it. That number is a 1 with 27 zeroes after it
1,000,000,000,000,000,000,000,000,000
or a billion billion billion.
The total number of possible arrangements of the air molecules in a room divided into two equal parts is
2N = 21027
or 2 raised to the power of a billion billion billion. It’s an absurdly large number.
There are still only two possible ways for all of the air molecules to be on one side of the room or the other, so the probability of finding a room in a state in which all of the air molecules are, by random chance, on one side of the room or the other is 2 out of 21027. To say that this is an extremely improbable state is beyond understatement.
In fact, by any reasonable definition, we can say that it’s effectively impossible for the air molecules in a room to spontaneously arrange themselves to be on just one side of the room. The usual course of things is for the air molecules to be very evenly distributed. But notice that it’s not strictly impossible to transgress this usual course of things. The probability of finding the air molecules on one side of the room by chance is extremely, extremely low, so low that we would never expect it to happen in the normal course of nature, but the probability is not precisely zero.
This toy model neglects other important physical effects, like enthalpy, but it suffices to demonstrate the point that a lot of physical systems are well described by probabilities. Personally, I think this is how God has built leeway into the system of the universe to do the seemingly impossible in the natural world without actually violating the laws of nature. It’s God, or an agent of God, doing what’s effectively impossible. In other words, impossible without intervention—like Eddie Tipton and his intervention in the lottery system—so, therefore, not impossible for God.
Let’s consider a biblical example, like the parting of the Red Sea. In Exodus 14, Moses is described as stretching out his hand at God’s command and parting the Red Sea so that the multitudes of people of Israel could cross it and escape from the pursuing Egyptians. This is referenced later in Deuteronomy 26:8 as one of the “signs and wonders” (oth and mopheth) God used to display his power and free Israel from Egypt. The probability of finding the waters of the Red Sea spontaneously parting on their own would be as exceptionally low as in our example of the air molecules in the room spontaneously arranging themselves on just one side. It’s so low that we would never expect it to happen in the usual course of nature, but, as we saw in the example of air molecules, it’s not strictly impossible.
Now, don’t misunderstand me. I am not:
claiming that all physical miracles have a foundation in probability. The miracle (semeion) of Jesus turning water into wine would involve a different physical mechanism than that illustrated by statistical thermodynamics.
claiming that all miracles are physical in character. Some miracles described in the Bible, such as the creation of the universe, the creation of life, and Jesus’ resurrection and ascension, are entirely supernatural in character.
attempting to explain miracles in a way that detracts from their wondrousness.
Given the absurd probabilities involved, that physical miracles can still fit into the natural framework of the universe makes them no less wondrous than if they defied the laws of nature.
By the mathematics of probabilities, it isn’t strictly impossible for someone with access to the lottery system to win the lottery. But, disregarding laws prohibiting employees of the lottery system from playing the lottery, wouldn’t we always be suspicious if such employees did win, even just once?
Now, what if an employee won the lottery twice? How about four times? The odds of winning the Mega Millions lottery four times in a row is approximately 1 out of 1025, about 100,000 times more probable than finding 100 air molecules on one side of a room. The odds are so overwhelmingly against a lottery employee winning by chance even just once, let alone four times, that it no one would believe it happened without someone interfering with the lottery system to force this outcome.
And isn’t that what we’re talking about with miracles?
According to the laws of physics, a miracle like parting the Red Sea doesn’t violate the laws of nature, it just requires a far greater level of influence with the forces of nature than we humans could ever have. It requires someone with access to the system to force an outcome that otherwise almost certainly wouldn’t happen.
In the next part, I’ll look at miracles from the perspective of the weird and wondrous world of quantum mechanics.








Super good stuff...thank you! Math/odds I get...we'll see how I do when we get to advanced class next week.